对数螺线

对数螺线的定义

对数螺线 又叫等角螺线。是自然界最常见的螺线形式。极坐标方程为$$r=ae^{b\theta}$$

取$a=0.01, b=0.2$，图形如下

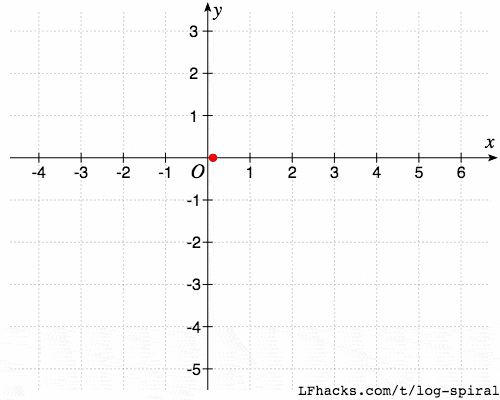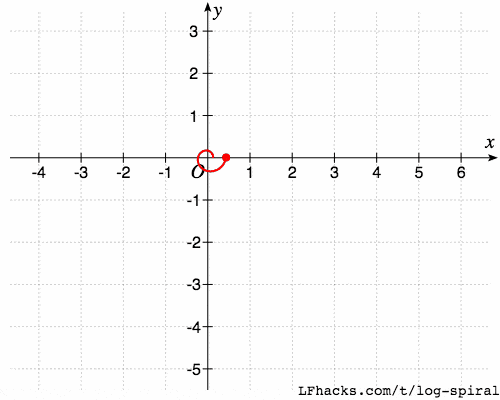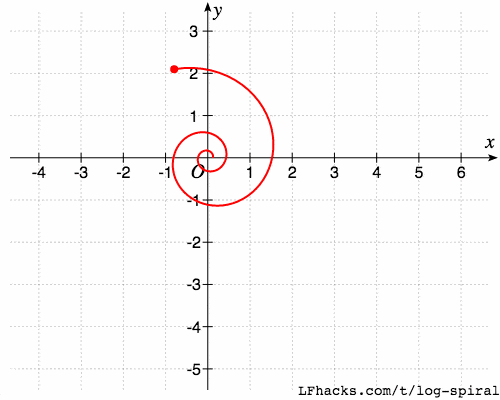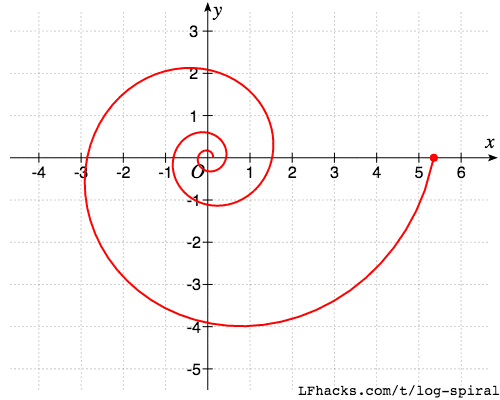
等角螺线

对数螺线也是等角螺线，有下面到性质：

原点出发的任意一条直线，与曲线所成角度 $\alpha$ 处处相等，且该角度为

$$\alpha=\arctan(1/b)$$

用图形解释，就是下图中两根蓝线的夹角始终不变。

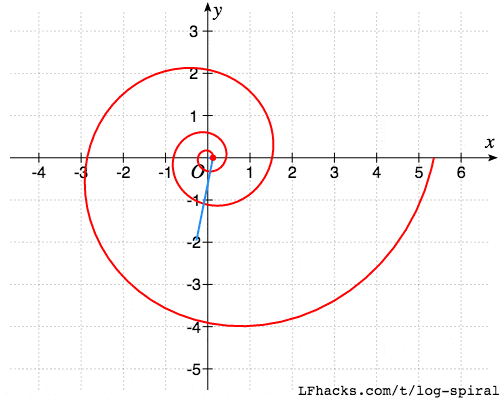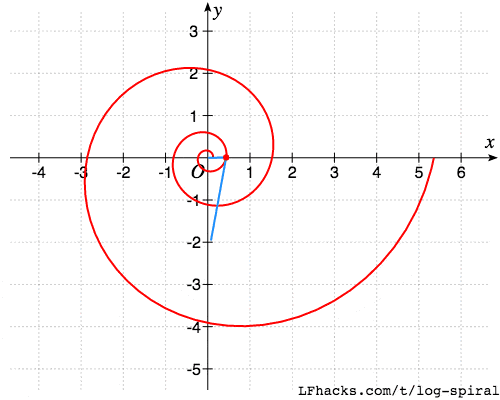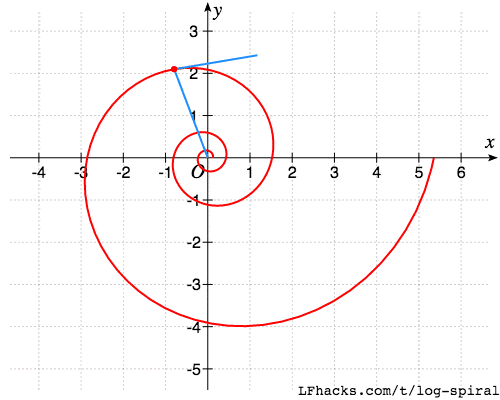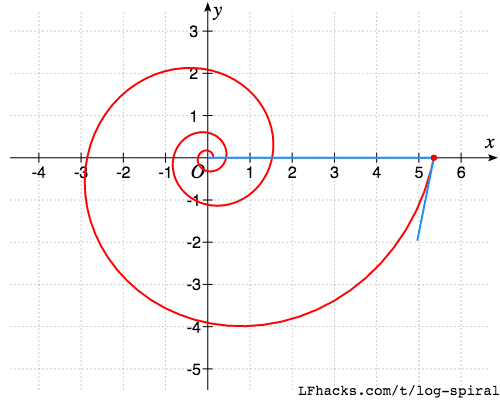
图中一条蓝线是从螺线上任意一点到原点的线段，另一条蓝线是螺线在该点的切线。

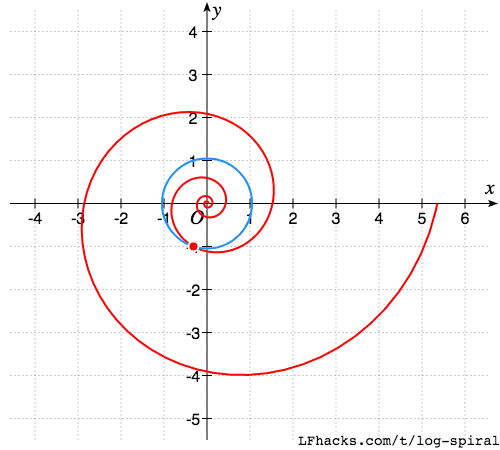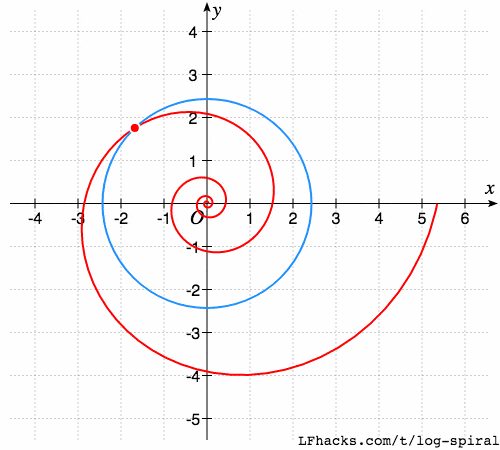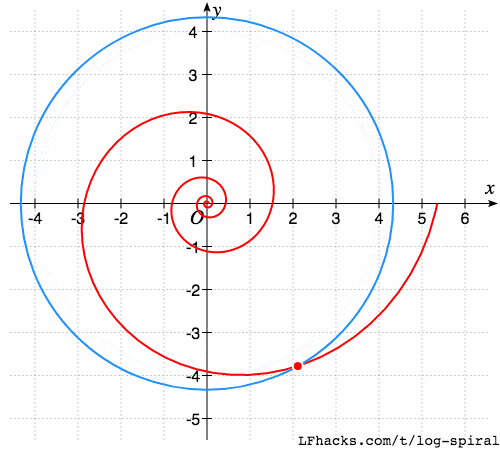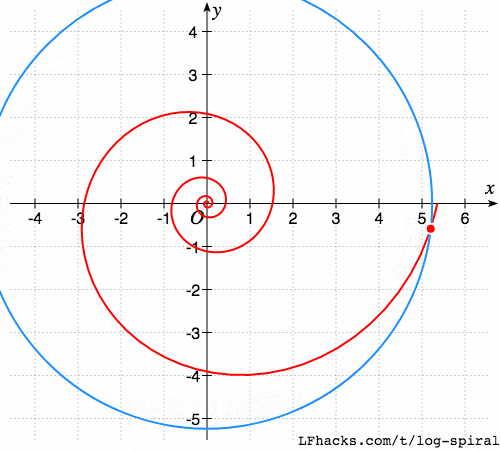
螺线与圆的夹角

以原点为圆心的任意圆，与等角螺线的相交的角，处处相等，

注意下图中红点两侧的夹角。

缩放的自相似性

放大和缩小后的对数螺线，和原图形相似，比如如下曲线族：

$$r(\theta)=ae^{b(A\theta)}$$

当 $A$ 逐步变化时，可以看出，图形完全重叠。

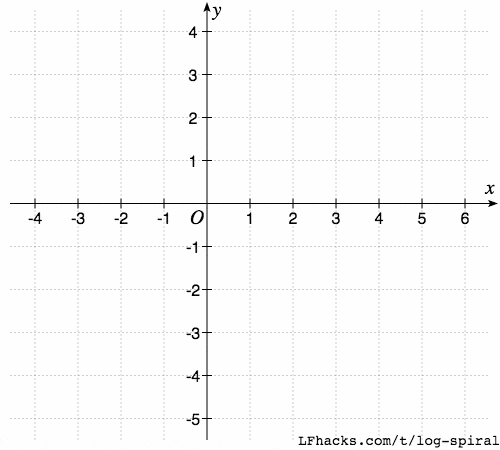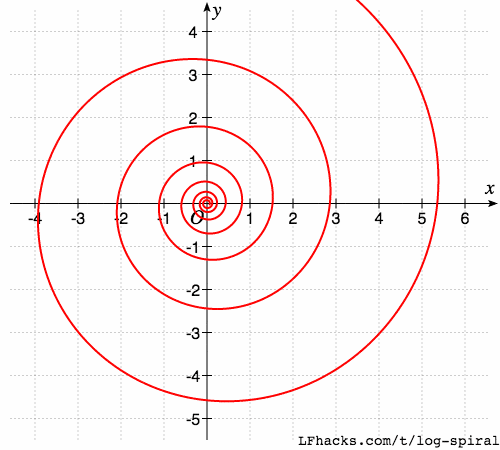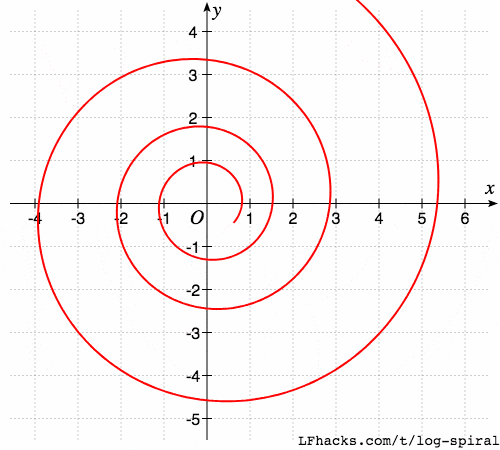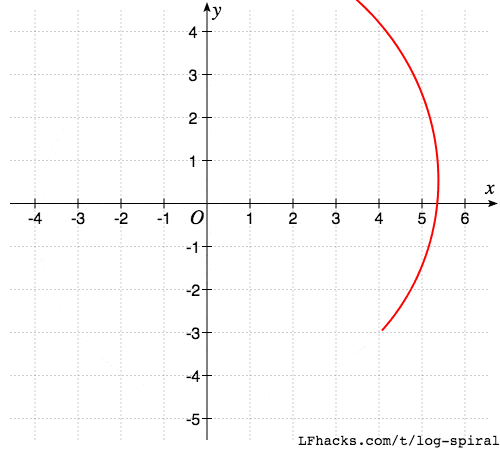
旋转的自相似性

旋转后的对数螺线，和原图形相似，比如如下曲线族：

$$r(\theta)=ae^{b(\theta+\delta)}$$

当 $\delta$ 逐步增大时，得到的图形如下。

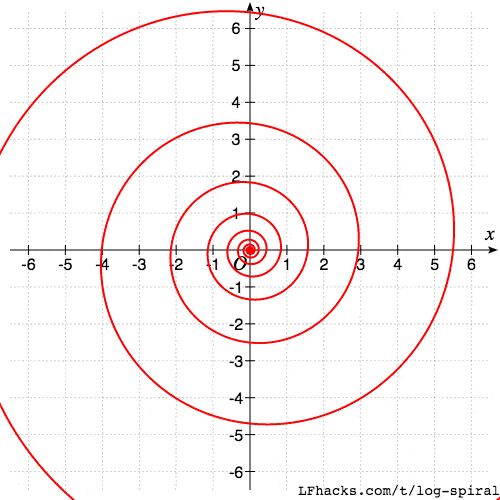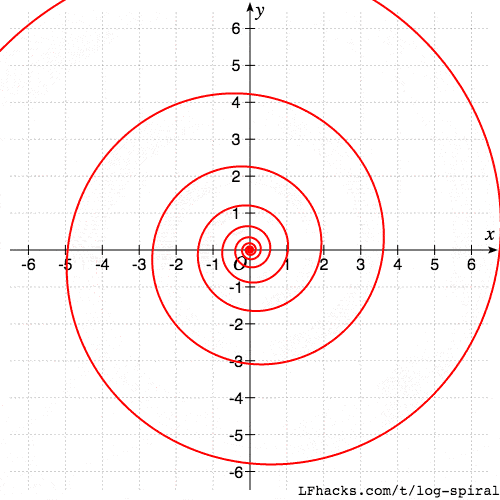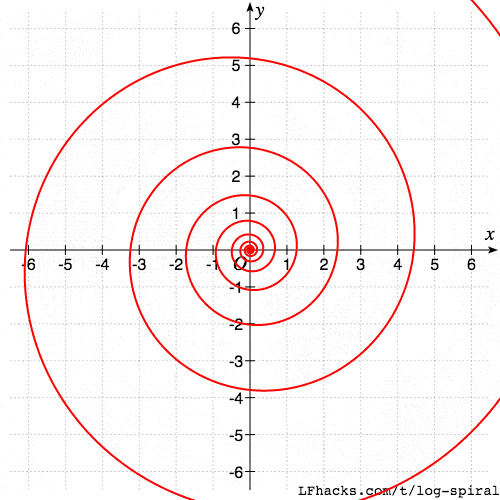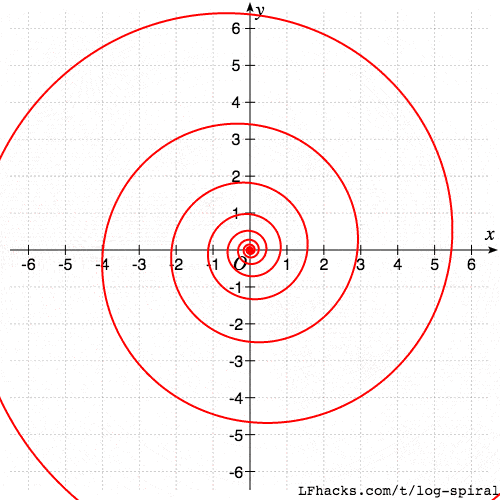
可以看出，得到的一族螺线是相似的。

墓志铭上的螺线

由于对数螺线具有上面许多美妙的性质，雅各布·伯努利 （Jacob Bernoulli，也就是伯努利双扭线 的那个伯努利，同时也是 伯努利实验的那个伯努利，但不是 伯努利定律 的那个伯努利，后者是前者的侄子）十分喜爱对数螺线，决定将对数螺线铭刻在自己的墓志铭上。见下图中的最下方：

可惜实际上工匠刻上了阿基米德螺线

如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论