形象解释
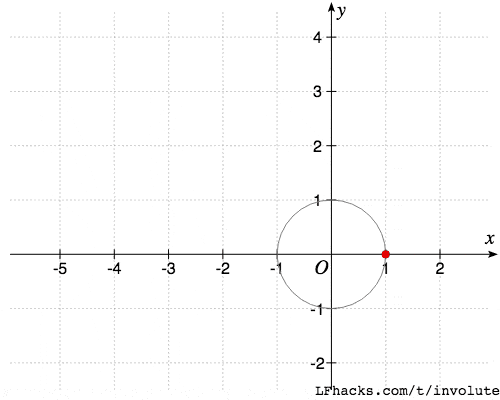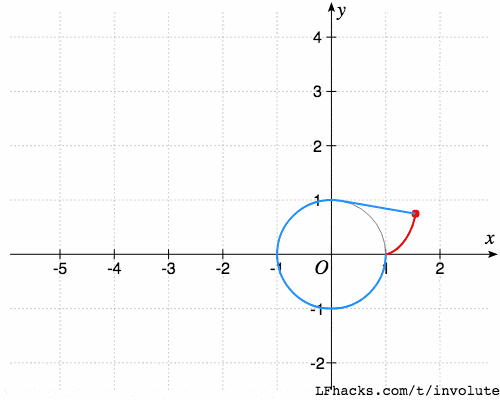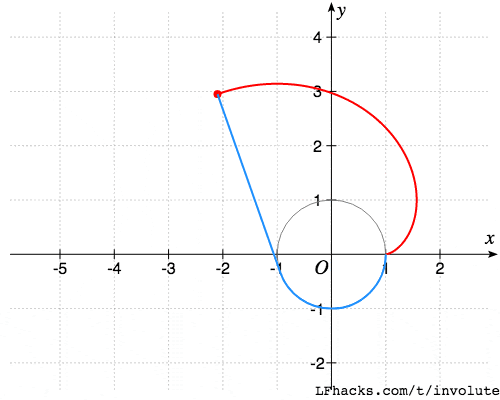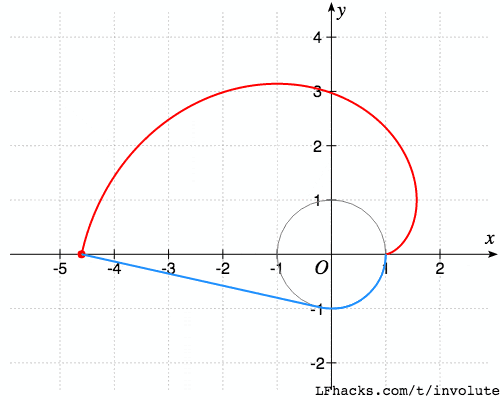
一条无伸缩的细绳绕在一个定圆上，拉开绳子的一端，使绳子与圆周始终相切，则直线上任意一点的轨迹，称为此基圆的一条渐开线。
方程
渐开线参数方程为$$x=a(\cos(t)+t\sin(t))\\y=a(\sin(t)-t\cos(t))$$
当渐开线延伸的角度 $t$ 越来越大后，圆的半径渐渐可以忽略。也就是上面方程式里的第一项相对 t 可以忽略，方程接近 $$x=at\sin(t)\\y=-at\cos(t)$$
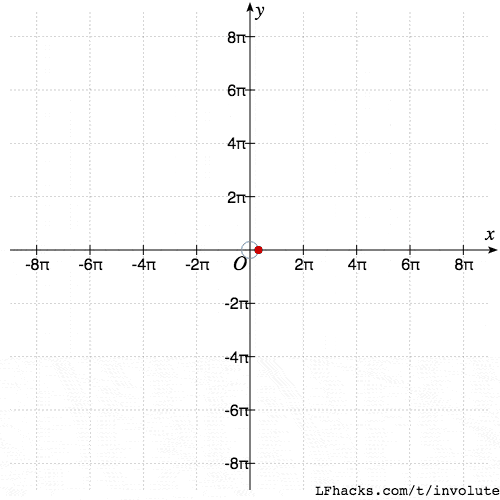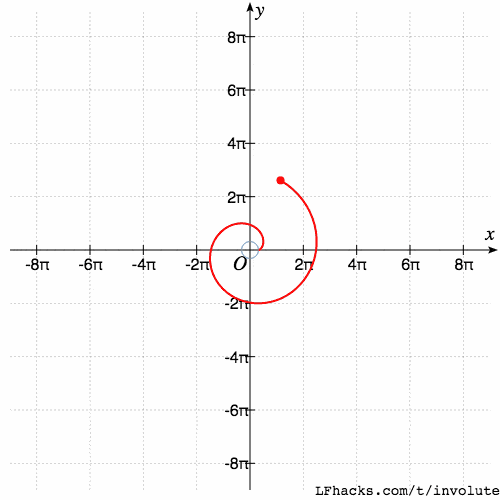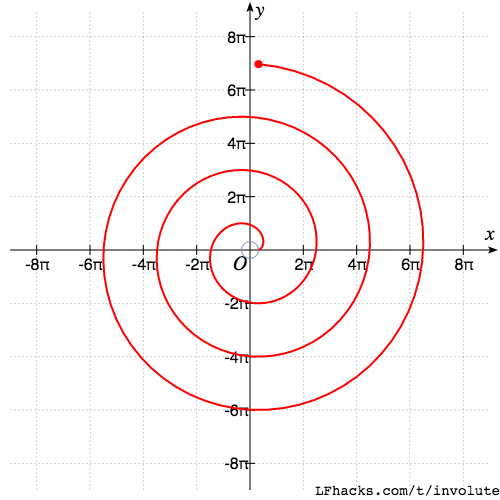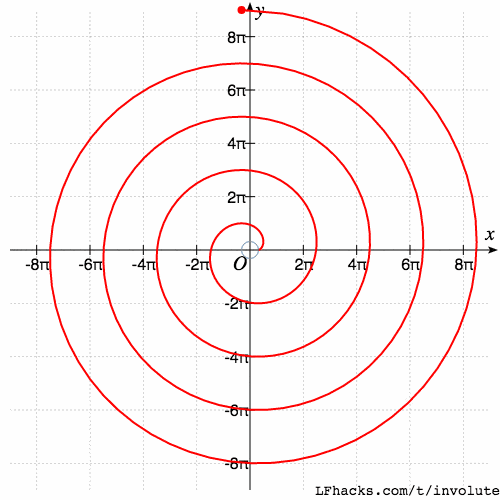
于是渐开线接近 阿基米德螺线,
如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板
标签： 曲线
给个免费的赞吧~
精彩评论
本站 是个人网站，采用 署名协议 CC-BY-NC 授权。
欢迎转载，请保留原文链接 https://www.lfhacks.com/t/involute/ ，且不得用于商业用途。