
用途
纽索纹(guilloche),也叫纽索饰。是在旋轮线、正弦曲线基础上,增加更多的细节控制,得到美观、细密的图形。
由于纽索纹的参数较多,且曲线的形状对参数非常敏感,仅从图形外观上不能反推得到参数值,于是难以复制,适合防伪用途。在装饰、防伪印刷品经常能看到纽索纹的身影:
(RMB 100元背面)
(身份证)
(证书边框)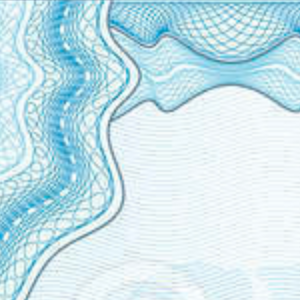
(防伪标志)
(香烟封条)
如何得到纽索纹
纽索纹 和 旋轮线 类似,都是在圆的参数方程基础上,通过以下步骤得到:
- 使极径 $ \rho$ 成为极角的函数$ \rho(t)$。
- $\rho(t)$是周期函数
- $\rho(t)$的周期不能被 $2\pi$ 整除
半径为 $R$ 的圆,方程为
$$\begin{cases} x(t) = R \cos(t) \\ y(t) = R \sin(t) \end{cases}$$
需要找到合适的极径函数 $\rho(t)$,得到$$\begin{cases} x(t)=\rho(t)\cos(t)\\y(t)=\rho(t) \sin(t)\end{cases}$$
$\rho(t)$称为受调制的极径。
基本图形
取极径函数 $$\rho(t)=R-r \cos(bt)$$ 得到: $$\begin{cases}x(t)=[R-r\cos(bt)] \cos(t)\\y(t)=[R-r \cos(bt)] \sin(t)\end{cases}$$
若取 $R=8, r=1, b=6$ 时,图形会是这样:
多个周期重复
为了生成 这一节 中交叉格子的图案,需要把周期缩小到 $2 \pi$ 以内,并且周期不能被 $2 \pi$ 整除。经过多个旋转周期后,不同周期的曲线自身相交叉得到格子图案。
$$\begin{cases} x(t)=[R-r \cos(b t)] \cos(a t)\\y(t)=[R-r \cos(b t)] \sin(a t), a<1 \end{cases} $$ 比如 $R=8,r=3,b=5,a=0.95,0<t<2\pi$ 时,曲线图形会是这样:
多周期重复后,得到
若取 $R=8, r=2, b=6, a=0.99, 0<t<2n\pi, 0<n<35, n\in\mathbb{Z}$时,图形会是这样:
图形对 a 值的敏感程度
图形对 $a$ 值的敏感程度,可以从下图看出:
取 $ a={0.999-0.001n|0 \le n \le 29, n\in\mathbb{Z}}$ 的30个数,相当于 $3 \% $ 的变化范围,$0<t<20\pi$.
可以看出图形发生了的很大的变化。$a$ 值的作用,是决定了图形的旋转角度,或者相位累积。
图形对 b 值的敏感程度
图形对 $b$ 值的敏感程度,可以从下图看出:取 $b=1\sim30$ 的30个数,$0<t<4\pi$. 可以看出 $b$ 值的作用,是决定了图形的极径函数 $\rho(t)$ 的基本频率。

图形对 r 值的敏感程度
图形对 $r$ 值的敏感程度,可以从下图看出:取 $R=9.7,p=0.5,a=0.825,b=3,0<r<200,0<t<30\pi$. 可以看出 $r$ 值的作用,是决定了图形的极径函数 $\rho(t)$ 的平均值。

精细调制
增加一项较低频率的振荡项。极径函数为
$$\rho(t)=R-r\cos(bt)-p\cos(ct),$$得到:$$x(t)=[R-r\cos(bt)-p\cos(ct)]
\cos(t)\\y(t)=[R-r\cos(bt)-p\cos(ct)] \sin(t)$$
若取 $R=8,r=2,p=1.5,a=0.99,b=6,c=0.02,0<t<40\pi$时,图形会是这样:
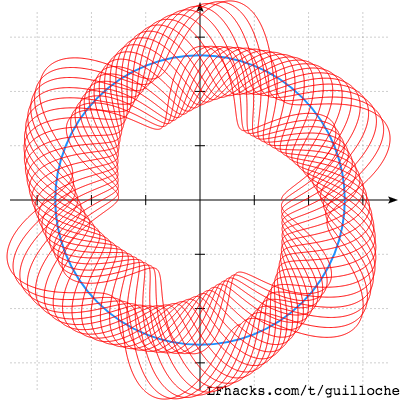
取 $c={0.01n|0<n<16, n\in\mathbb{Z}}$时,图形会是这样:

外摆线
从 有理数情况下的外摆线 入手,当 R 和 r 的比值 $R/r$ 接近随机数时,尖的数量增大很多,形成交叉格子的图案。
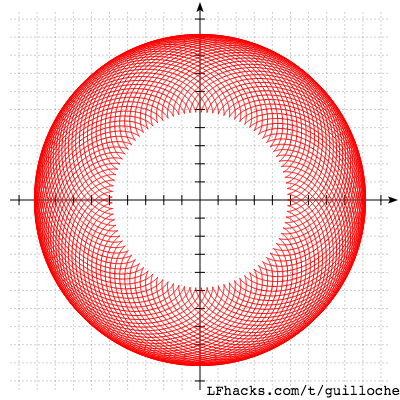
举个例子,若取 $R=9.7, r \in{4.7+0.02n|0<n<30, n\in\mathbb{Z}}$时,图形会是这样:
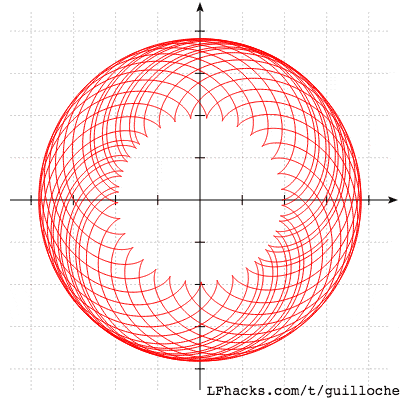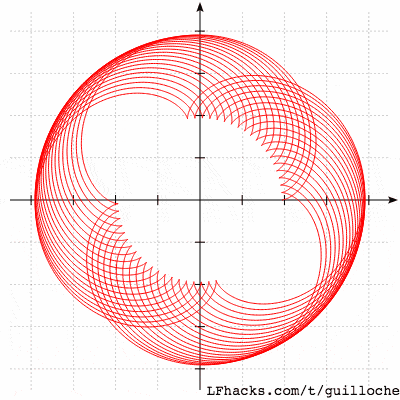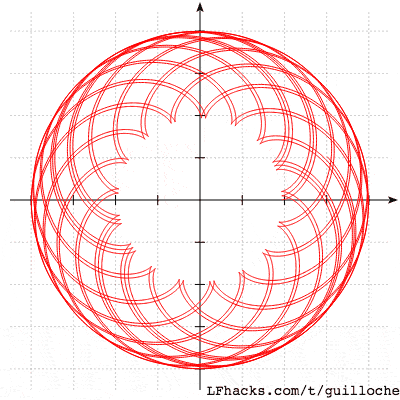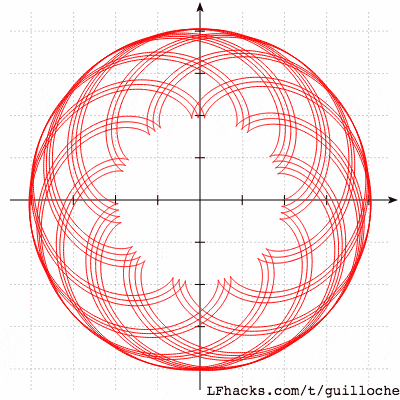
若取 $R=9.4, r \in{6+0.02n|0<n<30, n\in\mathbb{Z}}$时,图形会是这样:

例子
一张图模拟 防伪标志:
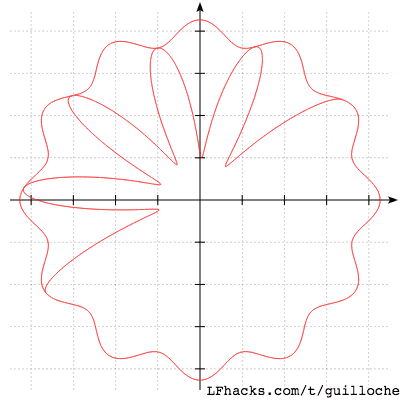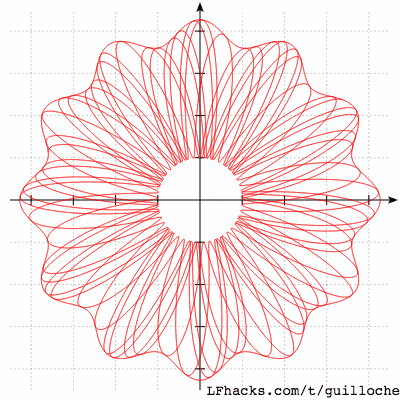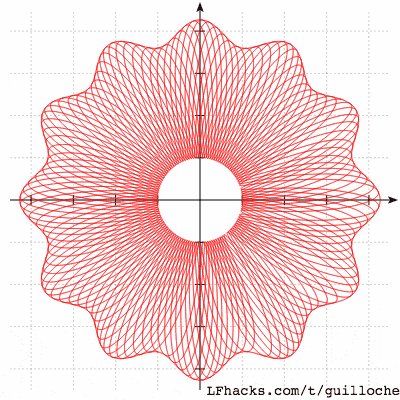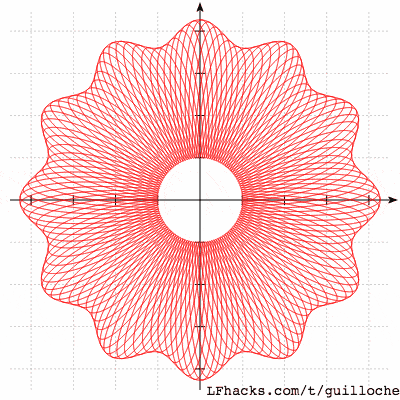
各位读后有什么想法,请在下方留言吧!如果对本文有疑问或者寻求合作,欢迎 联系邮箱 。邮箱已到剪贴板
精彩评论
本站 是个人网站,采用 署名协议 CC-BY-NC 授权。
欢迎转载,请保留原文链接 https://www.lfhacks.com/t/guilloche/ ,且不得用于商业用途。

